Freely Jointed Chain and Characteristic Ratio

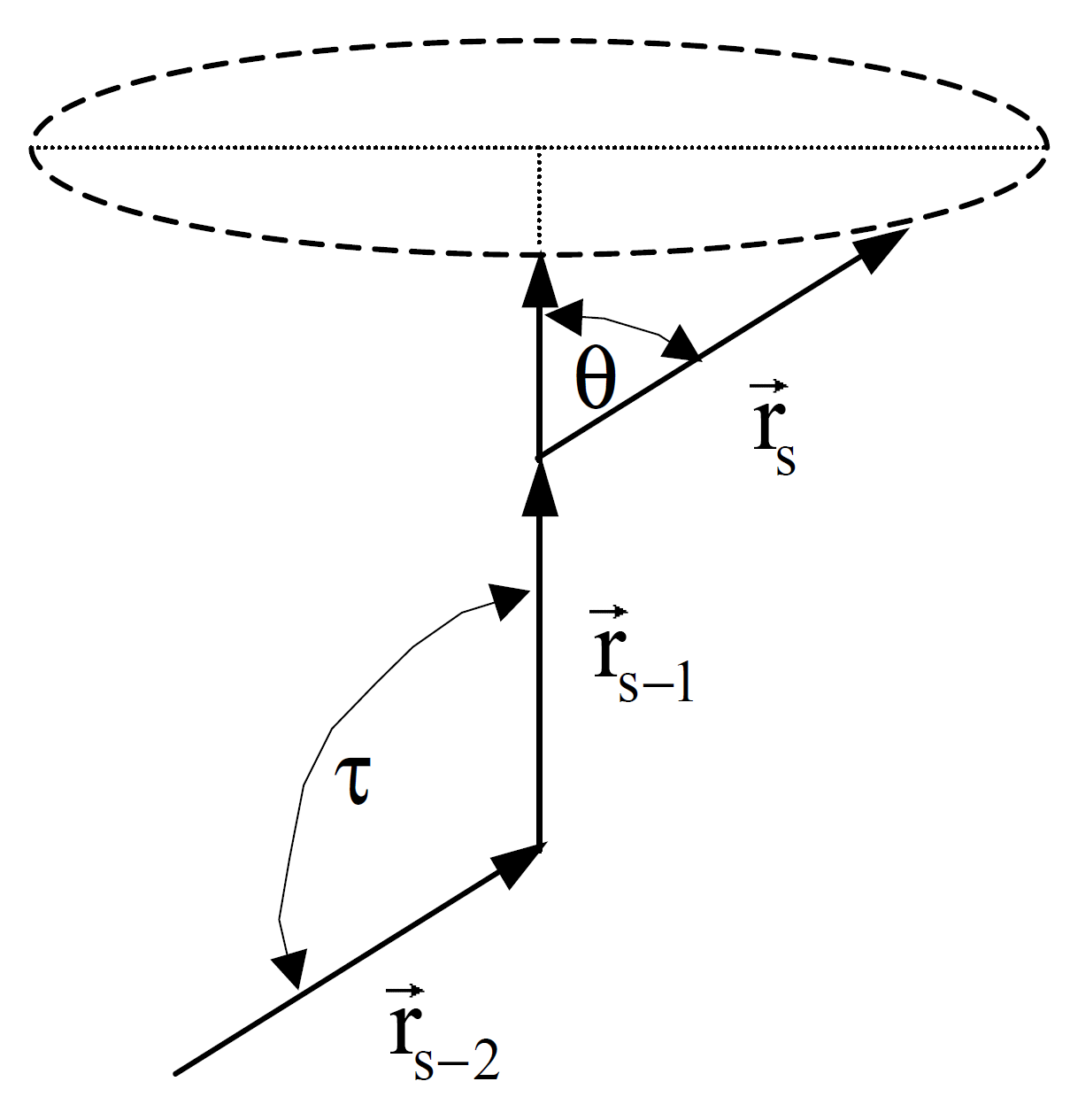
The idea to model a linear polymer chain as a freely jointed chain which occupies space as a random coil dates back to the 1930th when Kuhn1,2 defined a polymer chain as having NK rigid links of length lK with no restrictions on the angles between successive bonds. This model is a gross simplification of a real polymer chain because the rotation of real bonds is considerably restricted by fixed valence angles, τ, and by repulsive interactions with neighboring atoms along the polymer chain (steric hindrance). Nevertheless, Kuhn's polymer model of an equivalent freely jointed chain has been successfully used to describe the average behavior of real polymer chains in dilute solutions. To achieve equivalence, the N monomers of length l have to be replaced by statistical segments of length

lK = C∞l / sin(τ/2) = C∞l / cos(θ/2)

and the number of monomers in the chain has to be rescaled to the number of Kuhn monomers,3

NK = N /C∞ · cos(θ/2)2

The parameter C∞ is called the characteristic ratio which can be seen as a correction for the non-physical aspects of the freely jointed chain.

The length of a fully extended (rod-like) Kuhn model chain is identical with the contour length of the real chain:

Rmax = NK lK = N l · cos(θ/2)

As Kuhn and others have shown, the spatial properties of such a model chain are the same as those of a random flight in three dimensions. For example, the mean-square distance of the chain ends is given by

⟨R2⟩ = NK lK2

and the mean square radius of gyration8

⟨Rg2⟩ = NK lK2 / 6

Thus,

⟨R2⟩ = 6 ⟨Rg2⟩

The ratio of the mean-square distance and the contour length, ⟨R2⟩ / Rmax, is a measure for the stiffness of a polymer chain and is identical with the Kuhn length.3 For example, a polyethylene chain with bond length 1.54 Å, torsion angle 68°, and chanracteristic ratio = 6.74 has the Kuhn length

lK = ⟨R2⟩ / Rmax = C∞l / cos(θ/2) = 6.7 · 1.54 Å / cos(68°/2) = 12.4 Å

The concept of a Kuhn chain is quite useful for many model predictions. However, it is an oversimplification of a real polymer chain since we replaced the polymer with a hypothetical chain that behaves like a random-flight. By doing this, all information of the spatial arrangement of the real repeat units is lost.

References & Notes

  1. W. Kuhn, Kolloid Zeitschrift, 68, 2 (1934)

  2. W. Kuhn, H. Kuhn Helv. Chim. Acta, 26, 1394 (1934)

  3. These relationships follow from the two requirements that the contour length and the mean-square end-to-end distance have to be the same for the model chain and real chain:

    Rmax = NKlK = Nl sin(τ/2) = Nl cos(θ/2);   ⟨R2⟩ = NKlK2 = C∞Nl2

  4. Gert Strobl, The Physics of Polymers, 3rd Edition, Heidelberg 2007

  5. T. Hesse, Polymere an Phasengrenzflaechen, First Edition, Bremen 2004

  6. M. Rubinstein and R. Colby, Polymer Physics, 1st Ed., Oxford University Press, New York 2003

  7. The radius of gyration, Rg, is the average value of the first moment of all segments of the chain with respect to the center of mass of the molecule.

Revised May 31, 2021

  • Summary

    Freely Jointed Chain

    has the same spatial properties as a random flight in three-dimensions which is equivalent to that of the Brownian motion of a free particle.

  • The Kuhn length, lK, and the characteristic ratio, C∞, are both measures of the flexibility of a polymer chain. The lower these values are, the more ductile a polymer.

  • Flexible chains have characteristic ratios close to unity, while
    semiflexible and rigid polymers have very large values.

  • The smaller the characteristic ratio, the more a real polymer resembles a freely-rotating model chain.

  • The ultimate limit of the characteristic ratio is two, C∞ = 2.

      C∞ Table     

      lp Table